A Stick Slides Down A Wall
Weird animal, I want to crawl into my burrow and die, but the nearest thing on offer is gray midday and a bed, so I take it, and like Belacqua I think how very nice it is not to have to move. Think of a stick sliding down a wall. Play it in your head like a dumb movie and wonder: what is the path traced by this sliding stick of constant length? It starts out vertical and ends horizontal, and it must trace a curve on the way, but how is that curve defined? It would look something like a quarter circle, but that’s not right; even lying near-dead in bed, you can see the radius won’t stay constant. Get up and go downstairs to make coffee.
As the hapless line segment, length 1, proceeds down its catastrophe:
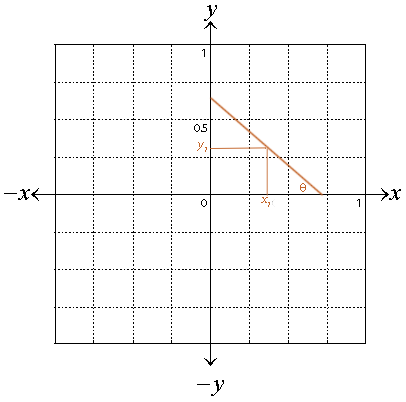
any point along its length with coordinates (x1, y1) will, by simple trig, satisfy
.gif)
But the curve of the entire catastrophe (sipping more coffee) isn’t trivial to calculate, since one’s choice of point will be independent of the value of θ. The height of the curve at any given x1 will be the maximum y1 possible as θ varies. Remember from a hot and dubious junior year in Tucson that you can get a local maximum by setting the first derivative to zero, thus
.gif)
which, remitted to our earlier equation, yields
.gif)
Drawing a right triangle is enough to work out that
.gif)
implying the monster
.gif)
which, surprisingly, reduces to the pleasing
.gif)
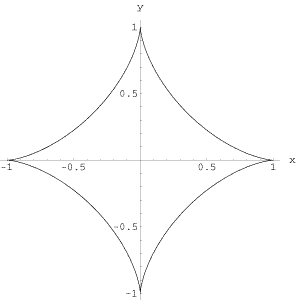
I graphed it on the iPhone, to see if it really looked like a stick sliding down a wall. It did.
(Omitted from the narrative is a half hour of biting the pen and getting trigonometric identities wrong while one’s daughter tried to steal one’s glasses, one’s coffee, one’s notebook; family life is a daily grace but people don’t talk about how, even in the center of love, it makes you feel inhumanly weak, sends you back to bed, you have to grasp for any beauty at hand to pull yourself back out.)
Formally, this is an algebraic curve of degree six, and one website can be trusted to keep a list of such things. Today’s visitor was an astroid, and can also be constructed by rolling wheels within wheels. Is it not lovely?